3.11 Fartsgrenser

Problem og formål
En av de faktorer som i sterkest grad påvirker antall ulykker og ulykkenes alvorlighetsgrad er trafikkens gjennomsnittsfart. Økt fart reduserer sikkerhetsmarginene under kjøring, ved at føreren tilbakelegger en større avstand før han eller hun rekker å reagere på en fare, og fordi feilmarginene blir mindre når føreren reagerer på en fare. Noen førere vil hevde at de er mer våkne og raskere til å reagere når de kjører fort enn når de kjører sakte. Simulatorstudier (Törnros, 1995) gir litt støtte til dette, men forskjellene i reaksjonstid er uhyre små og ingen førere kan kompensere for høyere fart ved å reagere raskere og riktigere.
For å sikre en forsvarlig avveining mellom ønsket om å komme fort fram og ønsket om få ulykker, er fartsgrenser innført i alle land. Bare deler av motorvegnettet i Tyskland har fri fart. Norge har hatt fartsgrenser på alle offentlige veger siden 1912. Mange andre motoriserte land har i lange perioder hatt fri fart på deler av vegnettet.
Fartsgrenser angir høyeste tillatte kjørefart. Formålet med fartsgrenser er å forebygge at førere utsetter seg selv og andre for høy risiko ved å kjøre uforsvarlig fort, samtidig som man tillater en tilstrekkelig høy fart til at en veg kan fylle sin transportfunksjon på en adekvat måte.
Beskrivelse av tiltaket
Det skilles mellom to typer fartsgrenser: Generelle og særskilte. De generelle fartsgrenser er i Norge fastsatt i vegtrafikkloven og er 50 km/t i tettbygde strøk og 80 km/t utenfor tettbygd strøk. Generelle fartsgrenser skiltes vanligvis ikke, men det er etter hvert blitt vanlig å skilte fartsgrense 50 km/t. Andre fartsgrenser enn de generelle kan innføres for bestemte vegstrekninger eller til bestemte tider av den som har myndighet til å vedta særskilte fartsgrenser. Særskilt fartsgrense skal alltid skiltes. For riks- og fylkesveger gjaldt følgende fartsgrenser i 2015 (Høye, 2016):
| Fartsgrense (km/t) | Veglengde (km) |
| 110 | 152 |
| 100 | 205 |
| 90 | 847 |
| 80 | 33458 |
| 70 | 1849 |
| 60 | 8060 |
| 50 | 4524 |
| 40 | 864 |
| 30 | 276 |
Fartsgrensen 110 km/t ble innført i 2014 på de beste motorvegene. Dette er samtidig de vegene som har mest trafikk av alle veger i Norge. Fartsgrenser under 50 km/t er innført på riks- og fylkesveger som går i boligområder der beboerne ofte ønsker lav fart. Det foreligger ingen landsomfattende oversikt over fartsgrenser på kommunal veg. Mange kommunale veger ligger i tettbygd strøk og betjener boligområder. Atkomstveger i boligområder har ofte fartsgrense 30 km/t. Større bygater har som regel fartsgrense 50 km/t.
I tillegg til de fartsgrenser som er angitt over, er to typer tidsbegrensede fartsgrenser innført i Norge. Det er vinterfartsgrenser på veger der ulykkesrisikoen om vinteren er høyere enn normalt. Vinterfartsgrensene er 10 km/t lavere enn sommerfartsgrensene. Dessuten er miljøfartsgrenser innført om vinteren på hovedveger i Oslo for å redusere spredning av partikler som slites løs ved kontakt mellom bildekk og vegdekket. Miljøfartsgrensen er 60 km/t. Sommerfartsgrense på de veger i Oslo som har miljøfartsgrense om vinteren er 70 eller 80 km/t.
Virkning på ulykkene
Sammenhengen mellom fart og risiko for skader og ulykker
Gjennom en serie undersøkelser, er det utviklet en modell som beskriver sammenhengen mellom fart og risiko for skader eller ulykker (Elvik, 2005, 2009, 2012, 2013, 2014, 2017, 2018, 2019; Elvik, Christensen & Amundsen, 2004; Elvik, Vadeby, Hels & van Schagen, 2019; Cameron & Elvik, 2010). Til sammen har disse studiene oppsummert resultater av mer enn 150 studier med mer enn 550 anslag på sammenhengen mellom fart og skader eller ulykker.
Den mest nyanserte og anvendelige statistiske modellen av sammenhengen mellom fart og skader eller ulykker er en eksponentialfunksjon som er føyd til en normalfordeling inndelt i 12 intervaller, der risikoen for skader eller ulykker varierer avhengig av fartsnivået og skadenes eller ulykkenes alvorlighetsgrad. Modellen skiller mellom følgende skader og ulykker:
- Drept
- Hardt skadet (meget alvorlig og alvorlig)
- Lettere skadet
- Personalskadeulykker
Det er vurdert som lite aktuelt å utvide modellen til materiellskadeulykker, siden forebygging av slike ulykker ikke er prioritert i myndighetenes trafikksikkerhetspolitikk.
Risikoen for skader eller ulykker settes lik én ved trafikkens gjennomsnittsfart. Trafikanter som holder høyere fart enn trafikkens gjennomsnittsfart har høyere risiko for skader eller ulykker, trafikanter som holder lavere fart har lavere risiko. På denne måten fanger risikokurvene opp både variasjon i den enkelte førers risiko avhengig av hvilken fart føreren velger og variasjon i det totale antallet skader eller ulykker som følge av endringer i trafikkens gjennomsnittsfart eller fordelingen av fart rundt gjennomsnittet. Modellen kan benyttes til å beregne følgende endringer i fart:
- En ensartet endring i fart i hele fartsfordelingen (det vil si at alle trafikanter endrer sin fart akkurat like mye, med samme antall kilometer per time)
- En større reduksjon av høye fartsnivåer enn av lave fartsnivåer
- En endring av fordelingen av førere mellom ulike intervaller i fartsfordelingen
- En endring av fartsspredning rundt en gitt gjennomsnittsfart.
Figur 3.11.1 viser hvordan risikoen for skader og personskadeulykker varierer avhengig av fart. Fartsgrense 80 km/t er brukt som eksempel. Gjennomsnittsfarten i 2017 var 76,1 km/t på veger med fartsgrense 80 km/t.
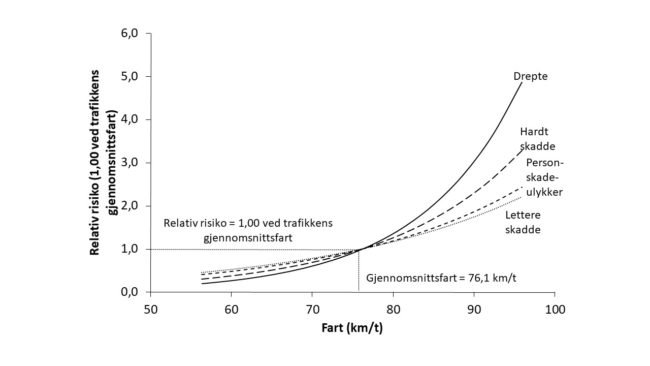
Figur 3.11.1: Skade- og ulykkesrisiko som funksjon av fart (fartsgrense 80 km/t).
Risikoen for å bli drept har den sterkeste sammenhengen med fart. Når farten er lik gjennomsnittet for øverste intervall i fartsfordeling (mellom 2,5 og 3 standardavvik over gjennomsnittet), 95,9 km/t, er relativ risiko for å bli drept 4,87, når risikoen settes lik 1,00 ved trafikkens gjennomsnittsfart. Når farten er lik gjennomsnittet i det laveste intervallet av fartsfordelingen (mellom 2,5 og 3 standardavvik under gjennomsnittet), 56,3 km/t, er relativ risiko for å bli drept 0,21. Høyeste risiko (4,87) er 23,2 ganger høyere enn laveste risiko (0,21). For lettere skadde er høyeste relative risiko (2,21) bare 4,9 ganger høyere enn laveste relative risiko (0,45).
Tabell 3.11.1 viser i detalj modellens oppbygging. Første kolonne viser intervallene i fartsfordelingen. Det er forutsatt at hele fartsfordelingen ligger mellom 3 standardvik under gjennomsnittet og 3 standardavvik over gjennomsnittet. Neste kolonne viser andelen i prosent av fartsfordelingen som ligger hvert intervall. Disse andelene bygger på en forutsetning om at fart er normalfordelt. Man kan velge en annen forutsetning ved å endre prosentandelen i hvert intervall av fordelingen, eksempelvis ved å forutsette at fordelingen har en «hale» av førere som holder høy fart. Prosentene må imidlertid i sum bli 100 og gjennomsnittsfarten må ikke endres.
Tredje kolonne viser gjennomsnittsfart i hvert intervall av fartsfordelingen. For å beregne gjennomsnittsfarten i hvert intervall må man kjenne standardavviket i fartsfordelingen. I offentlig tilgjengelige fartsdata oppgis ofte gjennomsnittsfart og 85 % fraktil (den fart 85 % holder seg under). Differansen mellom 85 % fraktil og gjennomsnitt, dividert på 1,04, er et godt anslag på standardavviket (i en normalfordeling tilsvarer gjennomsnittet pluss ett standardavvik 84,1 % fraktilen).
Relativ risiko i hvert fartsintervall er beregnet ved å benytte eksponentialmodellen med koeffisienter på 0,08 for drepte, 0,06 for hardt skadde og 0,04 for lettere skadde (0,045 for personskadeulykker). Relativ risiko for dødelig skade i øverste fartsintervall blir da:
Relativ risiko = = 4,87
Ved fart som er lavere enn gjennomsnittet, blir differansen i den indre parentesen i formelen negativ og relativ risiko blir lavere enn gjennomsnittet.
Tabell 3.11.1: Oppbygging av generell modell for beregning av virkninger av endring i fart.
| Intervall (standard-avvik) | Andel av fordelingen | Gjennom-snittsfart | Relativ risiko for dødelig skade | Bidrag til antall drepte | Relativ risiko for hard skade | Bidrag til antall hardt skadde | Relativ risiko for lett skade | Bidrag til antall lett skadde |
| 2.5-3 over | 0,6 % | 95,9 km/t | 4,874 | 2,92 | 3,281 | 1,97 | 2,208 | 1,32 |
| 2.5-2 over | 1,7 % | 92,3 km/t | 3,655 | 6,21 | 2,643 | 4,49 | 1,912 | 3,25 |
| 2-1.5 over | 4,4 % | 88,7 km/t | 2,740 | 12,06 | 2,130 | 9,37 | 1,655 | 7,28 |
| 1.5-1 over | 9,2 % | 85,1 km/t | 2,054 | 18,90 | 1,716 | 15,49 | 1,433 | 13,19 |
| 1-0.5 over | 15,0 % | 81,5 km/t | 1,540 | 23,11 | 1,383 | 20,74 | 1,241 | 18,62 |
| 0.5-0 over | 19,1 % | 77,9 km/t | 1,155 | 22,06 | 1,114 | 21,28 | 1,075 | 20,53 |
| 0-0.5 under | 19,1 % | 74,3 km/t | 0,866 | 16,54 | 0,898 | 17,14 | 0,931 | 17,77 |
| 0.5-1 under | 15,0 % | 70,7 km/t | 0,649 | 9,74 | 0,723 | 10,85 | 0,806 | 12,09 |
| 1-1.5 under | 9,2 % | 67,1 km/t | 0,487 | 4,48 | 0,583 | 5,36 | 0,698 | 6,42 |
| 1.5-2 under | 4,4 % | 63,5 km/t | 0,365 | 1,61 | 0,470 | 2,07 | 0,604 | 2,66 |
| 2-2.5 under | 1,7 % | 59,9 km/t | 0,274 | 0,47 | 0,378 | 0,64 | 0,523 | 0,89 |
| 2.5-3 under | 0,6 % | 56,3 km/t | 0,205 | 0,12 | 0,305 | 0,18 | 0,453 | 0,27 |
| Sum / gjennomsnitt | 100,0 % | 76,1 km/t | 1,000 | 118,21 | 1,000 | 109,88 | 1,000 | 104,28 |
Et relativt antall drepte, hardt skadde og lettere skadde er beregnet ved å gange relativ risiko med andelen av trafikken i hvert intervall og deretter summere tallene for alle intervaller. I øverste intervall blir dette for drepte: 4,874 ∙ 0,6 = 2,92. Summen blir mer enn 100, fordi økningen i risiko ved fart over gjennomsnittet er brattere enn nedgangen i risiko ved fart under gjennomsnittet.
Beregnede virkninger av ulike endringer i fart og fartsfordeling
Elvik (2019) illustrerer bruk av modellen som er forklart over til å beregne forventede virkninger av fire ulike endringer av gjennomsnittsfart og fartsfordeling. Disse endringene er oppsummert i tabell 3.11.2.
Tabell 3.11.2: Beregnede virkninger på antall drepte av fire endringer i gjennomsnittsfart og fartsfordeling (Elvik, 2019).
Type fartsendring |
Gjennomsnittsfart før (km/t) | Gjennomsnittsfart etter (km/t) | Nedgang i antall drepte (%) |
| Alle senker farten med 6 km/t | 76,1 | 70,1 | 38,1 |
| De som kjører over fartsgrensen reduserer farten; mest ved høyest fart | 76,1 | 73,8 | 29,1 |
| Andelen av førere i høye fartsintervaller reduseres; tilsvarende økning i lave intervaller | 76,1 | 75,3 | 8,2 |
| Standardavviket reduseres fra 7,2 til 5,0 km/t; uendret gjennomsnittsfart | 76,1 | 76,1 | 8,3 |
Det første tilfellet tilsvarer den typiske virkningen av nedsettelse av fartsgrensen. Det andre tilfellet tilsvarer virkningen av automatisk trafikkontroll. Siden de høyeste fartene reduseres mest, blir virkningen på antall drepte større enn endringen i gjennomsnittsfart isolert sett tilsier (som i eksemplet over er en reduksjon av antall drepte på 16,8 %). Det tredje tilfellet tilsvarer konvensjonell politikontroll. Også i dette tilfellet blir beregnet nedgang i antall drepte større enn endringen i gjennomsnittsfart tilsier. I det fjerde tilfellet reduseres kun spredningen i fart. Gjennomsnittsfarten er uendret. Det er likevel beregnet en nedgang i antall drept på litt mer 8 %. Denne nedgangen skyldes i sin helhet at mindre fartsspredning betyr at de høyeste fartene reduseres.
Fartsutviklingen i Norge og dens betydning for drepte og skadde
Tall som dekker perioden 2006 til 2017, innhentet til bruk i en undersøkelse om prinsipper for fastsetting av fartsgrenser (Elvik, 2017), viser at trafikkens gjennomsnittsfart er redusert fra 2006 til 2017 for alle fartsgrenser unntatt 100 km/t. Fartsgrensen 110 km/t har eksistert for kort til at man kan si noe fartsutviklingen over tid.
Beregning med eksponentialmodellen tyder på at nedgangen i fart ved de fleste fartsgrenser fra 2006 til 2017 har redusert antall drepte i denne perioden med 20 %, antall hardt skadde med 16 % og antall lettere skadde med 11 %. I samme periode viste trendlinjer føyd til data for perioden 2000-2017 en nedgang i antall drepte fra 2006 til 2017 på 48,5 %, en nedgang i antall hardt skadde på 34,4 % og en nedgang i antall lettere skadde på 41,7 %. Dette innebærer at lavere fart forklarer ca. 41 % av nedgangen i antall drepte, ca. 47 % av nedgangen i antall hardt skadde og ca. 26 % av nedgangen i antall lettere skadde.
Sammenhengen mellom endring av fartsgrenser og endring av trafikkens gjennomsnittsfart
En endring av fartsgrensen fører ikke alltid til at trafikkens gjennomsnittsfart endres like mye. Hvis man, for eksempel, senker fartsgrensen fra 80 til 70 km/t går trafikkens gjennomsnittsfart som oftest ikke ned med 10 km/t, men viser en mindre endring. Sammenhengen mellom endringer av fartsgrense og endringer av trafikkens gjennomsnittsfart, basert på 143 resultater, er vist i figur 3.11.2.
I de aller fleste tilfeller endres trafikkens fart i samme retning som fartsgrensen, det vil si at den øker når fartsgrensen settes opp og synker når fartsgrensen settes ned. Ved økning av fartsgrensen øker trafikkens fart vanligvis mye mindre enn økningen i fartsgrense, typisk med rundt regnet 5 km/t dersom fartsgrensen settes opp med 20 km/t.
Når fartsgrensen settes ned, synker nesten alltid trafikkens gjennomsnittsfart. Nedgangen i fart øker jo mer fartsgrensen settes ned og er i gjennomsnitt om lag 8 km/t når fartsgrensen settes ned med 20 km/t. Nedsettelser av fartsgrensen har større virkninger på trafikkens gjennomsnittsfart enn tilsvarende økninger av fartsgrensen. Spredningen i resultater er imidlertid stor, både for økning av fartsgrensen og for nedsettelse av den.
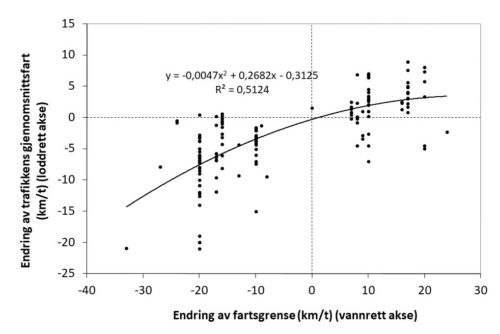
Figur 3.11.2: Sammenheng mellom endring av fartsgrense og endring av trafikkens gjennomsnittsfart.
Virkning på framkommelighet
Det er en direkte sammenheng mellom kjørefart og reisetid. Reisetiden er en invers funksjon av farten. Holder man en fart på 50 km/t, vil en tur på 100 km ta to timer. Økes farten til det dobbelte, 100 km/t, tar turen halvparten så lang tid, en time. Den høyeste fart trafikken avvikles med ligger omkring 130 km/t. Dette er trafikkens gjennomsnittsfart på tyske motorveger uten fartsgrense og på andre motorveger i Europa med fartsgrense 130 km/t når det er lite nok trafikk til at hvert kjøretøy kan velge fart uten å bli særlig påvirket av andre kjøretøys fart. I Norge var trafikkens gjennomsnittsfart på veger med fartsgrense 110 km/t i 2017 102,3 km/t.
Det er viktig å være klar over at reisetidsbesparelsen ved en gitt økning av fart synker jo høyere farten er i utgangspunktet. Man sparer 60 minutter på en 100 km strekning ved å øke farten fra 50 til 100 km/t. Ved å øke fra 100 til 150 km/t sparer man på den samme strekningen bare 20 minutter (det tar 40 minutter å tilbakelegge 100 km i en fart på 150 km/t).
Virkning på miljøforhold
I en analyse av fartsgrensepolitikk (Elvik, 2017) ble miljøkostnadene per kjøretøykilometer beregnet som funksjon av fart, basert på økonomiske verdsettinger anbefalt i Statens vegvesens håndbok V712, Konsekvensanalyser (Statens vegvesen, 2014). Miljøkostnadene omfatter kostnader ved utslipp av NOx og PM10 (mikropartikler), CO2 (global oppvarming) og trafikkstøy. Kostnadene som funksjon av fart ved fartsgrensene 50 og 80 km/t er vist i figur 3.11.3.
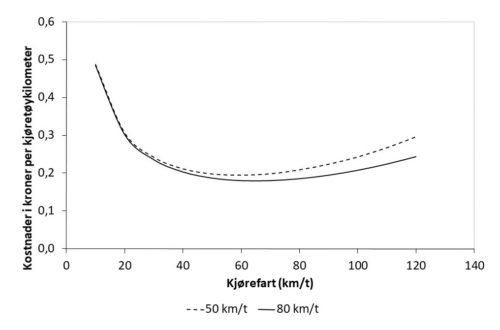
Figur 3.11.3: Miljøkostnader per kjøretøykilometer ved fartsgrense 50 og 80 km/t som funksjon av kjørefart.
Miljøkostnadene øker litt mer ved høyere fart ved fartsgrense 50 km/t enn ved fartsgrense 80 km/t. Dette skyldes økte støykostnader ved høyere fart. Støy representerer en høyere kostnad i byer og tettsteder enn i spredtbygd strøk.
Kostnader
Kostnadene ved å ha generelle fartsgrenser er minimale, siden disse fartsgrensene er fastsatt i vegtrafikkloven og for det meste ikke blir skiltet. Ved innføring av særskilt fartsgrense, må denne skiltes. Skiltene må gjentas etter hvert kryss. Kostnadene til skilting av særskilte fartsgrenser utgjør i størrelsesorden 15.000-20.000 kr. per kilometer veg. Dette gjelder kostnader til oppsetting av skilt. I tillegg kommer saksbehandlingskostnader under planlegging av innføring av særskilt fartsgrense. Disse kostnadene er ikke godt kjent, men dersom man antar en saksbehandlingstid på ett ukeverk til en timekostnad på 1.000 kroner, blir kostnaden ca. 40.000 kroner for hvert vedtak som fattes om en særskilt fartsgrense.
Nytte-kostnadsvurderinger
I en studie av fartsgrensepolitikk, ble tre prinsipper for fastsetting av fartsgrenser sammenlignet (Elvik, 2017):
- Nullvisjonsfartsgrenser
- Samfunnsøkonomisk optimale fartsgrenser
- Et troverdig fartsgrensesystem
Nullvisjonsfartsgrenser bygger på Nullvisjonens biomekaniske grunnlag. Dette er formulert i form av kurver som viser sannsynligheten for varig skade ved tre ulykkestyper: fotgjenger som påkjøres av bil, sidekollisjoner mellom biler (med samme masse) og frontkollisjoner mellom biler (med samme masse). Kritisk fart ved disse tre ulykkestypene er beregnet til, henholdsvis, 30, 50 og 70 km/t. Av dette følger at høyeste fartsgrense der hvor fotgjengere kan bli påkjørt er 30 km/t; høyeste fartsgrense der hvor biler kan sidekollidere er 50 km/t og høyeste fart der hvor frontkollisjoner kan forekomme er 70 km/t. Hvis frontkollisjoner er hindret i form av midtdeler eller midtrekkverk, kan vegen ha en høyere fartsgrense enn 70 km/t.
Samfunnsøkonomisk optimale fartsgrenser fastsettes slik at summen av alle kostnader ved en kjøretøykilometer minimeres. De samfunnsøkonomiske kostnadene inkluderer tidskostnader, kjøretøys driftskostnader, ulykkeskostnader, global oppvarming, lokal forurensning og støy.
Et troverdig fartsgrensesystem innebærer at flertallet av trafikantene forstår og godtar hvorfor ulike fartsgrenser er fastsatt. Høy troverdighet bidrar til økt overholdelse av fartsgrensene og kan dermed reduseres behovet for kontroll.
Tabell 3.11.3 viser fartsgrenser fastsatt etter disse prinsippene. Veger med fartsgrense 80 km/t er omfattende og uensartede. I analysen ble disse vegene derfor delt i tre grupper. En gruppe med høy risiko for alvorlige ulykker (omkring 30 % av dagens 80-veger); en gruppe med normal risiko, men ikke midtrekkverk (knapt 70 % av dagens 80-veger) og en gruppe med midtrekkverk (omkring 1 % av dagens 80-veger).
Tabell 3.11.3: Fartsgrenser fastsatt etter tre ulike prinsipper.
| Dagens fartsgrenser | Nullvisjons-fartsgrenser | Optimale fartsgrenser | Troverdige fartsgrenser |
| 30 km/t | 30 km/t | 60 km/t | 30 km/t |
| 40 km/t | 40 km/t | 70 km/t | 40 km/t |
| 50 km/t | 40 km/t | 70 km/t | 50 km/t |
| 60 km/t | 50 km/t | 70 km/t | 60 km/t |
| 70 km/t | 70 km/t | 80 km/t | 70 km/t |
| 80 km/t høy risiko | 70 km/t | 70 km/t | 70 km/t |
| 80 km/t uten midtrekkverk | 70 km/t | 80 km/t | 80 km/t |
| 80 km/t med midtrekkverk | 90 km/t | 90 km/t | 90 km/t |
| 90 km/t | 90 km/t | 100 km/t | 100 km/t |
| 100 km/t | 100 km/t | 100 km/t | 110 km/t |
| 110 km/t | 110 km/t | Ikke beregnet | 110 km/t |
Nullvisjonsfartsgrenser er for det meste lavere enn dagens fartsgrenser eller lik dagens fartsgrenser. Eneste unntak er 80-veger med midtrekkverk, der fartsgrensen ifølge Nullvisjonen kan være høyere enn 80 km/t, eksempelvis 90 km/t. Det ble beregnet at innføring av Nullvisjonsfartsgrenser kunne redusere antall drepte med 20-38 per år (14-26 %), avhengig av hvor godt fartsgrensene overholdes. Antall hardt skadde kunne reduseres med 69-134 (10-20 %) per år, avhengig av respekten for fartsgrensene.
Samfunnsøkonomisk optimale fartsgrenser er i de fleste tilfeller høyere enn dagens fartsgrenser. En innføring av slike fartsgrenser vil derfor føre til flere drepte og skadde i trafikken, selv om farten neppe ville øke like mye som fartsgrensene ble satt opp. Innføring av samfunnsøkonomisk optimale fartsgrenser er i konflikt med målet om å redusere antall drepte og hardt skadde i trafikken.
I en oppfølgende analyse (Elvik, 2018) ble det påvist at de samfunnsøkonomisk optimale fartsgrenser har økt over tid. Det er to hovedgrunner til det. Den første er at skaderisikoen per kjøretøykilometer er betydelig redusert over tid. Ulykkeskostnadene per kjørt kilometer er dermed blitt mye lavere enn de var for 20-25 år siden og teller mindre i de totale samfunnsøkonomiske kostnader ved trafikken. Den andre hovedgrunnen er at den økonomiske verdsettingen av spart reisetid har økt mer enn ulykkeskostnadene. Dermed teller spart reisetid mer og mer i regnestykkene.
Jo lavere skaderisikoen i trafikken blir, desto høyere vil optimale fartsgrenser bli. Å innføre optimale fartsgrenser vil dermed reversere tendensen til lavere risiko i trafikken. Gitt at målet er det motsatte – å redusere skaderisikoen – kan en tradisjonell beregning av samfunnsøkonomisk optimale fartsgrenser ikke lenger sies å gi noen relevant veiledning for bruk av fartsgrenser som trafikksikkerhetstiltak.
Kan lave fartsgrenser, særlig i byer og tettsteder, i det hele tatt begrunnes samfunnsøkonomisk? Elvik (2018) viser at tradisjonelle beregninger av optimale fartsgrenser er mangelfulle, siden bare motorisert trafikk inngår i dem. I byene er det et mål at flere skal gå eller sykle, og lave fartsgrenser kan bidra til dette målet. Lave fartsgrenser gjør bilkjøring mindre attraktivt og kan dermed bidra til at noen slutter å kjøre bil og heller velger å gå eller sykle. Regne-eksempler viser at helsegevinsten ved at flere går eller sykler kan tenkes å være større enn det nyttetapet bilistene påføres ved at fartsgrensen i byer er lav, eksempelvis 30 km/t. Det kan følgelig ikke utelukkes at en fartsgrense på 30 km/t er samfunnsøkonomisk lønnsom når også gang- og sykkeltrafikk tas med i regnestykket.
Troverdige fartsgrenser antas å ligge nær dagens fartsgrenser, dog med visse unntak. Økning av fartsgrensen på motorveg til 110 km/t har bred støtte. I dag har ikke alle motorveger denne fartsgrensen. Nedsettelse av fartsgrensen fra 80 til 70 km/t på veger med høy risiko kan også bli oppfattet som troverdig, spesielt hvis det inngår i en pakke av fartsgrenseendringer som også omfatter økning av fartsgrensen på veger der det er forsvarlig. Ved at endringene går både opp og ned skaper man bedre muligheter til å begrunne endringene og øker dermed sjansen for at trafikantene ser dem som troverdige.
Formelt ansvar og saksgang
Initiativ til tiltaket
Generelle fartsgrenser er fastsatt i vegtrafikkloven. De generelle fartsgrenser er 80 km/t i spredtbygd strøk og 50 km/t i byer og tettsteder. Initiativ til fastsetting av særskilte fartsgrenser kan bli tatt av vegmyndighetene eller av lokale interesser.
Vedtak om høyere fartsgrenser enn det som følger av vegtrafikkloven treffes av Statens vegvesen ved Vegdirektoratet. Øvrige fartsgrensevedtak treffes av Statens vegvesen for riks- og fylkesveg og av kommunen for kommunal veg.
Formelle krav og saksgang
Statens vegvesen har utarbeidet kriterier for fastsetting fartsgrenser på alle offentlige veger (Statens vegvesen, 2018). Kriteriene gjelder fra 1.11.2018. I tillegg til disse kriteriene, er formelle krav til fartsgrenser fastsatt i Vegnormalene (Statens vegvesen, håndbok N100, 2019) og Skiltnormalene (Statens vegvesen, håndbok N300, 2012). Skiltnormalene inneholder også tekniske krav til utforming av trafikkskilt.
Ansvar for gjennomføring av tiltaket
Myndigheten til å fastsette fartsgrenser er fordelt mellom flere organer. Bestemmelser om dette står i skiltforskriften § 26.
Fartsgrense skiltes med skilt 362, fartsgrense, og oppheves med skilt 364, slutt på fartsgrense. Kostnader til skilting av fartsgrense dekkes av staten for riksveg, fylkeskommunen for fylkesveg, kommunen for kommunal veg og grunneier for privat veg.
Referanser
Cameron, M. H., Elvik, R. 2010. Nilsson’s Power Model connecting speed and road trauma: Applicability by road type and alternative models for urban roads. Accident Analysis and Prevention, 42, 1908-1915.
Elvik, R. 2005. Speed and road safety. Synthesis of evidence from evaluation studies. Transportation Research Record, 1908, 59-69.
Elvik, R. 2009. The Power Model of the relationship between speed and road safety. Update and new estimates. Report 1034. Oslo, Institute of Transport Economics
Elvik, R. 2012. Speed limits, enforcement, and public health consequences. Annual Review of Public Health, 33, 225-238.
Elvik, R. 2013. A re-parameterisation of the Power Model of the relationship between the speed of traffic and the number of accidents and accident victims. Accident Analysis and Prevention, 50, 854-860.
Elvik, R. 2014. Fart og trafikksikkerhet. Nye modeller. Rapport 1296. Oslo, Transportøkonomisk institutt.
Elvik, R. 2017. Miniscenario: Fartsgrensepolitikk. Rapport 1589. Oslo, Transportøkonomisk institutt, 2017.
Elvik, R. 2018. How can the notion of optimal speed limits best be applied in urban areas? Transport Policy, 68, 170-177.
Elvik, R. 2019. A comprehensive and unified framework for analysing the effects on injuries of measures influencing speed. Accident Analysis and Prevention, 125, 63-69.
Elvik, R., Christensen, P., Amundsen, A. H. 2004. Speed and road accidents. An evaluation of the Power Model. Report 740. Oslo, Institute of Transport Economics.
Elvik, R., Vadeby, A., Hels, T., van Schagen, I. 2019. Updated estimates of the relationship between speed and road safety at the aggregate and individual levels. Accident Analysis and Prevention, 123, 114-122.
Høye, A. 2016. Utvikling av ulykkesmodeller for ulykker på riks- og fylkesvegnettet i Norge (2010-2015). Rapport 1522. Oslo, Transportøkonomisk institutt.
Statens vegvesen. 2012. Håndbok N300 Trafikkskilt. Oslo, Statens vegvesen, Vegdirektoratet.
Statens vegvesen. 2014. Håndbok V712 konsekvensanalyser. Oslo, Statens vegvesen, Vegdirektoratet (oppdatert utgave utgitt i 2018, men 2014-utgaven ble brukt i undersøkelsen det henvises til)
Statens vegvesen. 2018. NA-rundskriv 2018/10 Fartsgrensekriterier. Oslo, Statens vegvesen, Vegdirektoratet.
Statens vegvesen. 2019. Håndbok N100 Veg- og gateutforming. Oslo, Statens vegvesen, Vegdirektoratet.
Törnros, J. 1995. Effect of driving speed on reaction time during motorway driving. Accident Analysis and Prevention, 27, 435-442.

