2.2 Utbedring av ujevnhet og spor i vegdekket

Ujevnhet og spor i vegdekket kan føre til at førere mister kontroll over kjøretøyet, de kan forårsake skader på kjøretøy, og fører ofte til at farten settes ned.
Veger med større ujevnheter har i de aller fleste studiene flere ulykker enn jevnere veger. Ulykkesøkningen er som regel større ved større ujevnhet, mens det er ingen eller liten sammenheng mellom ujevnhet og ulykker på svært jevne veger (ujevnhet, målt som IRI, under 3 mm/meter). Den gjennomsnittlige relative ulykkesrisikoen, i forhold til IRI = 1 (som er en svært jevn veg), er på 1,51 ved IRI = 4 og, på 2,49 ved IRI = 6, og betydelig høyere ved høyere IRI. Det er imidlertid relativt stor variasjon mellom resultatene fra de enkelte studiene. Sammenhengen mellom ujevnhet og ulykker er trolig større for eneulykker enn for flerpartsulykker, og større på tofeltsveger enn i kryss og på flerfeltsveger.
Økende spordybde har i en rekke studier vist seg å medføre flere ulykker. Ved en spordybde på 8 mm øker antall ulykker med 50-150 prosent i forhold til veger uten spor. Dette gjelder imidlertid ikke i kryss; her medfører økende spordybde i gjennomsnitt færre ulykker. På veger utenom kryss ble det funnet større ulykkesøkninger for eneulykker enn for flerpartsulykker. På våt veg medfører spor trolig større ulykkesøkninger enn på tørr veg.
Veger med en generelt god tilstand på vegdekket, har som regel færre ulykker enn dårlige veger. Ulykkene kan imidlertid være mer alvorlige på bedre vegdekker, trolig som følge av høyere fart. Motorsyklister har også høyere risiko på dårlige veger enn på gode vegdekker.
Problem og formål
Ujevnheter i vegdekket kan medføre økt ulykkesrisiko, øke slitasjen på kjøretøy og de kan skade kjøretøy. Vann som samles i spor i vegdekket øker faren for vannplaning.
Statens vegvesens dybdestudier av dødsulykker i vegtrafikken i 2005-2016 viser at andelen dødsulykker hvor spor i vegdekket har vært medvirkende faktor i ulykken, i gjennomsnitt var på 4,3 prosent. I de fleste årene var andelen mellom én og fem prosent, i 2009 var det 13 prosent.
I Norge er store andeler av vegnettet i relativt dårlig tilstand. Andelen av vegnettet hvor ujevnheten på tvers og/eller på langs er klassifisert som «dårlig eller svært dårlig», var i 2019 på 36 prosent på fylkesveinettet i region Øst og på rundt fem prosent på riksvegnettet i region Øst. På fylkesveinettet i region Øst hadde 32 prosent dårlig eller svært dårlig jevnhet på langs, og seks prosent hadde dårlig eller svært dårlig jevnhet på tvers (Statens vegvesen, 2019).
Utbedringer av ujevnhet og spor i vegdekket skal fjerne farlige ujevnheter og spor i vegdekket, slik at faren for å miste kontroll over kjøretøyet reduseres. Andre formål er å redusere slitasje på kjøretøy og dekk, og å øke framkommeligheten og kjørekomforten.
Beskrivelse av tiltaket
Spor og ujevnheter er elementer i vegdekkets megatekstur, dvs. variasjoner i jevnheten mellom 5 og 50 cm (Cairney & Styles, 2005). Ujevnheter er høydeforskjeller på langs og spor er høydeforskjeller på tvers av kjøreretningen på vegen. Spor og ujevnheter påvirker bl.a. kjørekomfort, slitasje på kjøretøyenes dempesystemer, kjøretøyenes sidestabilitet og bremselengden, samt vannavrenning. Med utbedring av vegdekkers ujevnhet og spordybde menes tiltak som bl.a. fylling av hull i vegdekket og sporfylling.
Alminnelig fornyelse av vegdekker, dvs. reasfaltering, som ofte medfører at vegdekket blir jevnere, er behandlet i kapittel 2.1. Mindre ujevnheter i vegdekket (0,5 mm til 5 cm) betegnes som makrotekstur og ujevnheter på under 0,5 mm betegnes som mikrotekstur. Virkninger av makro- og mikrotekstur på ulykker er beskrevet i kapittel 2.3 Bedring av vegdekkers friksjon.
Ujevnhet på langs (IRI)
Det mest vanlige mål for vegdekkets ujevnheter på langs er IRI (international roughness index). I Norge uttrykkes IRI normalt i millimeter vertikale avvik per meter veg. Det finnes mange ulike måter å måle IRI på. Bl.a. kan IRI måles manuelt med rettholt (linjal av en gitt lengde) ved at man legger dette på vegen (på langs med kjøreretningen) og måler det maksimale avvik mellom vegens overflate og rettholt (Statens vegvesen, 2021, R211). Dermed angir IRI hvor mye bilkarosseriet beveger seg vertikalt når bilen har kjørt 1 meter (Dysvik et al., 2020).
Andre definisjoner av IRI og målemetoder er beskrevet av Múčka (2017) og av Piryonesi og El-Diraby (2021). I USA er det vanlig å definere IRI som forhold mellom vertikale bevegelser i bilers støtdempersystem og lengden av kjørt strekning, som regel som inch per mil eller meter per kilometer. På nye veger ligger IRI som regel mellom 0,81 og 1,03 mm/meter (Piryonesi & El-Diraby, 2021). I empiriske studier som har undersøkt sammenhengen mellom IRI og ulykker, ligger IRI for det meste mellom én og syv mm/meter.
Ujevnheter øker som regel med økende alder på vegdekket (Christensen & Ragnøy, 2006; Abdelaziz et al., 2020; Al-Suleiman & Shiyab, 2003). Ujevnheter er også sterkt korrelert med spordybde, dvs. at vegdekker med større ujevnhet som regel også har dypere spor (Christensen & Ragnøy, 2006; Cairney & Bennett, 2008; Tehrani et al., 2012). Flere empiriske studier viser at ujevnheter øker fra år til år, men at dekkekvaliteten holder seg på et relativt høyt nivå de første 10-15 årene; etter det øker forfallet stadig mer fra år til år (Elghriany et al., 2016; Hicks et al., 1999).
Typiske verdier for IRI er ifølge Dysvik et al., (2020):
- Ny veg: Under 2,0
- Normal god standard: Mellom 2,5 og 3,5
- Eldre vegdekker: Mellom 3,5 og 6,0; IRI på 4,0 og høyere indikerer økende grad av ødelagt vegdekke.
Typiske terskelverdier som anses som minste akseptable verdier for IRI ligger som regel på mellom 1,7 og 2,6 (Arhid et al., 2015; Semnarshad et al., 2018). Terskelverdiene er lavere for motorveger enn for andre veger.
Statens vegvesens håndbok R610 (2012) spesifiserer krav til 90-persentilen av 20-meters IRI-verdier for strekninger på 1 km lengde (90-persentil betyr at 90 prosent av de målte verdiene er lavere). Disse varierer med ÅDT og vegdekkeklasse, fra 3,5 mm per meter på veger i vegdekkeklasse 1 (som bl.a. benyttes for riksveger) med ÅDT > 10.000 til 7,0 mm per meter på veger i vegdekkeklasse 2 og ÅDT <300. I tillegg kreves at ingen 20-meters verdi overskrider kravet med mer enn 3 mm per meter (unntatt på strekninger med f.eks. fartsdempere eller gatestein). På gang- og sykkelveger skal ujevnheter på langs, målt med 3 meter rettholt, være mindre enn 10 mm.
En kartlegging av ujevnheter på norske veger i 2014 (Nordahl, 2016; sitert etter Dysvik et al., 2020) viste at andelen av vegnettet som ikke oppfyller kravene i R610, er lavest på Europaveger (under 10 prosent i de fleste fylkene) og andre riksveger (under 30 prosent i de fleste fylkene), høyere på primære fylkesveger (mellom 19 og 48 prosent) og høyest på sekundære fylkesveger (mellom 54 og 85 prosent).
Spordybde
Spordybde er ujevnheter i vegdekket på tvers. Slike ujevnheter kan oppstå som følge av slitasje (i hovedsak fra piggdekk), komprimering eller sideforskyvning av masser (Statens vegvesen, 2018). Spor påvirker bilenes sidestabilitet, især under kjørefeltskifter (Anastasolpulos et al., 2012) og de kan også øke risikoen for vannplaning (Ding & Wang, 2018).
Spordybden kan bl.a. måles manuelt med rettholt (linjal av en gitt lengde) ved at man legger dette vegen (på tvers) og måler det maksimale avvik mellom vegens overflate og rettholt (Statens vegvesen, 2021, R211).
Statens vegvesens håndbok R610 (2012) spesifiserer krav til 90-persentilen av 20-meters spordybder for strekninger på 1 km lengde (90-persentil betyr at ku 10% av målingene viser en høyere verdi). Denne skal ikke være over 25 mm ved ÅDT under 5000 og ikke over 20 mm ved ÅDT over 5000. I tillegg kreves at ingen 20-meters verdi overskrider kravet med mer enn 40 mm.
På gang- og sykkelveger skal ujevnheter på tvers, målt med 3 meter rettholt, være mindre enn 15 mm.
Andre mål på vegdekkets tilstand
Det finnes ulike andre mål som beskriver kvaliteten på vegdekker som f.eks. «pavement serviceability index» og «pavement condition index». Slike mål henger ofte sammen med både spordybde og ujevnhet, men omfatter som regel flere aspekter enn disse som bl.a. større hull og krakelering.
Virkning på ulykkene
Ujevnhet (IRI) og ulykkesrisiko
Sammenhengen mellom ujevnheter i vegdekket og ulykker er undersøkt i de følgende studiene:
Al-Masaeid, 1997 (Jordan)
Christensen & Ragnøy, 2006 (Sverige)
Anastasopoulos et al., 2008 (USA)
Cairney & Bennett, 2008 (Australia)
Chan et al., 2009 (USA)
Tegge et al., 2010 (USA)
Ihs et al., 2011 (Sverige)
Tehrani et al., 2012 (Canada)
Buddhavarapu et al., 2013 (USA)
Li et al., 2013 (USA)
Pulugurtha et al., 2013 (USA)
King, 2014 (Australia)
Ma, Chen, & Chen, 2015 (USA)
Elghriany et al., 2016 (USA)
Ghanbari, 2017 (USA)
Hussein & Hassan, 2017 (Australia)
Sarwar et al., 2017 (USA)
Vinayakamurthy et al., 2017 (USA)
Xin et al., 2017 (USA)
Alhasan et al., 2018 (USA)
Hou et al., 2018A (Kina)
Hou et al., 2018B (Kina)
Mamlouk et al., 2018 (USA)
Chen et al., 2019 (USA)
Kuleno et al., 2019 (Etiopia)
Saeed et al., 2019 (USA)
Akbari et al., 2020 (Iran)
Appiah et al., 2020 (USA)
Lee et al., 2020 (USA)
Popoola et al., 2020 (Nigeria)
Bock et al., 2021 (USA)
Cafiso et al., 2021 (Italia)
Hussein et al., 2021 (Australia)
De aller fleste resultatene viser at økende ujevnheter medfører flere ulykker når man kontrollerer for trafikkmengden.
Det er imidlertid langt fra alle studier som har rapportert resultater som kan brukes som grunnlag for å beregne relative ulykkestall ved ulike verdier av IRI.
Figur 2.2.1 viser uvektede gjennomsnitt av estimerte relative ulykkestall ved IRI-verdier fra en til 10. Den relative risikoen er satt lik én ved IRI = 2. Resultatene er basert på 14 relative ulykkestall fra 10 studier for opptil IRI = 4; for høyere IRI foreligger færre resultater. IRI-verdier fra studier som har oppgitt IRI i inches per mil, er omregnet til mm per meter. Figuren viser kun resultater for alle ulykkestyper. Det er ikke skilt mellom ulike vegtyper (se nedenfor under Vegtype). Det er langt fra alle studiene som gjør det mulig å tallfeste virkningen av økende IRI på antall ulykker, og det er ikke tatt hensyn til den metodiske kvaliteten på studiene. Det er også stor spredning i resultatene. Resultatene i figur 2.2.1 må derfor tolkes med forbehold om noe usikkerhet.
De aller fleste resultatene som inngår i figur 2.2.1, viser at antall ulykker øker med økende IRI; kun ett resultat per IRI-verdi viser en nedgang av antall ulykker (Christensen & Ragnøy, 2006). I denne studien er den relative ulykkesrisikoen lik 0,93 ved IRI = 4 og lik 0,76 ved IRI = 10.
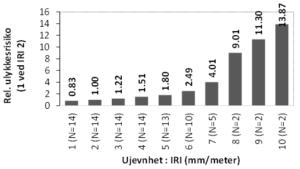
Figur 2.2.1: Uvektede gjennomsnitt av estimerte relative ulykkestall ved IRI-verdier; kun resultater som gjelder alle ulykkestyper.
Synkende ulykkestall med økende ujevnhet: Det er kun fire (av 33) studier som viser at antall ulykker går ned med økende IRI (Al-Masaeid, 1997; Christensen & Ragnøy, 2006; Appiah et al., 2020; Ghanbari, 2017). De fleste av disser resultatene gjelder enten eneulykker eller er basert på ulykker på mindre veger. Både for eneulykker og mindre veger viser resultatene fra andre studier at økende ujevnhet er mer uheldig (dvs. medfører større ulykkesøkninger).
Hvilken form har sammenhengen mellom ujevnhet og ulykker? Resultatene i figur 2.2.1 tyder på at antall ulykker øker mer med økende IRI ved høye IRI-verdier enn ved lavere verdier. Den største økningen finner man fra en IRI på syv. Tre studier som ikke inngår i figuren, viser at antall ulykker først begynner å øke fra en IRI på mellom 2,3 og 3,3, mens det ikke er noen tydelig sammenheng med lavere IRI-verdier (Elghriany et al., 2016; Vinayakamurthy et al., 2017; Mamlouk et al., 2018). En annen studie viser at den største målte IRI-verdien i et vegsegment har større sammenheng med antall ulykker enn gjennomsnittlig IRI (Tehrani et al., 2012).
To studier har funnet sammenhenger som har en omvendt U-form, dvs. at antall ulykker øker med økende IRI for lave IRI-verdier, og synker med økende IRI ved høyere IRI-verdier (Popoola et al., 2020; Pulugurtha et al., 2013). Disse resultatene må betraktes som utypiske da de fleste øvrige studiene viser at antall ulykker øker relativt jevnt med økende IRI, eller at antall ulykker først øker fra en viss terskelverdi.
For å oppsummere, tyder de fleste resultatene på at økende ujevnhet medfører større ulykkesøkninger ved høyere IRI-verdier, og at det ved lave IRI-verdier (IRI = 3 eller lavere) er ingen eller liten sammenheng mellom ujevnhet og ulykker.
Ulykkestyper: Hvilke ulykkestyper som påvirkes mest, spriker mellom studiene:
- Eneulykker øker mer med økende ujevnhet enn flerpartsulykker i tre studier (Cafiso et al., 2021; Chan et al., 2009; Lee et al., 2020)
- I studien til Ghanbari et al. (2017) medfører økende ujevnheter færre ulykker og nedgangen er større for flerpartsulykker enn for eneulykker, dvs. at økende ujevnhet er mindre gunstig for eneulykker enn for flerpartsulykker, noe som er konsistent med funnet i punktet over
- Flerpartsulykker øker mer med økende ujevnhet mens antall eneulykker går ned i studien til Al-Masaeid et al. (1997)
Alt i alt tyder dermed de fleste resultatene på at økende ujevnheter er mest ugunstige for eneulykker og at flerpartsulykker i mindre grad blir negativt påvirket.
Når man beregner gjennomsnittlige endringer av antall ulykker for alle resultatene samlet, øker antall eneulykker mer enn det totale antall ulykker opptil en IRI på fem, og antall flerpartsulykker øker i mindre grad. Ved høyere IRI øker derimot det totale antall ulykker i gjennomsnitt mer enn både ene- og flerpartsulykker. For IRI over fem foreligger imidlertid kun relativt få resultater, i de fleste studiene er de høyeste IRI-verdiene på fire eller fem.
Type kjøretøy: I studien til King (2014) medfører økende ujevnhet større ulykkesøkninger for ulykker med lette kjøretøy enn for ulykker med tunge kjøretøy.
Skadegrad: To studier har undersøkt sammenhengen for ulike skadegrader og begge viser at økende ujevnheter medfører en større økning av antall personskadeulykker enn av antall materiellskadeulykker (Chen et al., 2019; Saeed et al., 2019).
Våt vs. tørr veg: De aller fleste resultatene fra studiene som har undersøkt sammenhengen mellom ujevnhet og ulykker, gjelder alle ulykker, uansett om vegen er våt eller tørr. To studier som har undersøkt sammenhengen mellom IRI og ulykker på våt og tørr veg, spriker. Én av studiene viser at økende ujevnhet medfører ulykkesøkning på tørr veg men at det ikke er noen sammenheng på våt veg (Cafiso et al., 2021). En annen studie fant en større sammenheng mellom IRI og ulykker på våt veg enn på tørr veg, men dette gjelder kun ved svært lave IRI-verdier (1,5-2,7 vs. under 1,5; Pulugurtha et al., 2013).
Type veg: Når man deler inn resultatene i figur 2.2.1 etter type veg, finner man følgende relative ulykkestall ved IRI = 4 (høyeste IRI-verdi hvor det foreligger resultater for alle vegtyper):
- Alle veger: 1,83 (2 resultater)
- Motorveger: 1,42 (5 resultater)
- Andre flerfeltsveger: 1,16 (3 resultater)
- Tofeltsveger: 2,19 (3 resultater)
- Kryss: 1,19 (1 resultat).
Den relative ulykkesrisikoen på en helt jevn veger her satt lik én; risikoen er altså f.eks. 1,83 ganger så høy på en ujevn veg (med IRI = 4) enn på en helt jevn veg. Den største ulykkesøkningen ble funnet på tofeltsveger. På flerfeltsveger og i kryss er ulykkesøkningen betydelig mindre. At den minste økningen ble funnet i kryss, er konsistent med at virkningen er større på eneulykker enn på flerpartsulykker, da de fleste ulykkene i kryss er kollisjoner. De konkrete relative ulykkestallene kan likevel ikke uten videre generaliseres da de er basert på relativt få studier.
Typer veg – trafikkmengde: Økende ujevnhet medfører større ulykkesøkninger på veger med høy trafikkmengde i to studier (Hussein et al., 2021: kryss med gjennomsnittlig ÅDT 27.000; Lee et al., 2020: motorveger med gjennomsnittlig ÅDT 50.000).
Typer veg – fartsgrense: Økende ujevnhet medfører større ulykkesøkninger på veger med høy fartsgrense (Alhasan et al., 2018); dette gjelder tofelts-landeveger.
Spordybde og ulykkesrisiko
Sammenhengen mellom spordybde og ulykker er undersøkt i de følgende studiene:
Start, Kim & Berg, 1998 (USA)
Christensen & Ragnøy, 2006 (Sverige)
Anastasopoulos et al., 2008 (USA)
Cairney & Bennett, 2008 (Australia)
Chan et al., 2009 (USA)
Tegge et al., 2010 (USA)
Tehrani et al., 2012 (Canada)
Dong et al., 2015 (USA)
Hussein & Hassan, 2017 (Australia)
Sarwar et al., 2017 (USA)
Vinayakamurthy et al., 2017 (USA)
Alhasan et al., 2018 (USA)
Hou et al., 2018A (Kina)
Hou et al., 2018B (Kina)
Mamlouk et al., 2018 (USA)
Alacash & Perry, 2019 (UK)
Kuleno et al., 2019 (Etiopia)
Hussein et al., 2021 (Australia)
Resultatene spriker mye mellom studiene. De fleste studiene viser at økende spordybde medfører økende antall ulykker. Ved en spordybde på 8 mm er den gjennomsnittlige relative ulykkesrisikoen på 2,59 (relativ risiko ved en spordybde på 0 mm er satt lik én). Dette er et uvektet gjennomsnitt som er basert på 11 resultater fra syv studier som har rapportert tilstrekkelig informasjon for å beregne relative ulykkestall. De øvrige studiene har ikke oppgitt slik informasjon. Resultater for kryss er utelatt (se nedenfor).
Den relative ulykkesrisikoen er betydelig lavere (1,52) når man utelater resultater fra to studier som har funnet ekstremt store ulykkesøkninger.
Kryss: To av studiene har undersøkt sammenhengen mellom spordybde og ulykker i kryss, og begge viser at antall ulykker er omtrent uendret eller går ned med økende spordybde. I studien til Hussein et al. (2021) er det 30-40 prosent færre ulykker ved en spordybde på 8 mm enn ved 0 mm spordybde. I studien til Hussein & Hassan (2017) er antall ulykker omtrent uendret.
Ulykkestyper: Når man ser på veger utenom kryss, er den relative ulykkesrisikoen ved 8 mm spordybde på 2,35 for eneulykker og på 1,13 for flerpartsulykker. Dette tyder på at spordybde har større effekt (medfører større ulykkesøkninger) på eneulykker. Resultatet er imidlertid basert på få studier (ingen av de to resultatene som viser ekstremt store ulykkesøkninger, gjelder spesifikt for ene- eller flerpartsulykker).
Kurver: Hou et al. (2018A) viser at for vegdekker i motorvegtunneler har spordybde større sammenheng med antall ulykker i kurver enn på rette strekninger. Spordybde har også større sammenheng med antall ulykker i tunneler med en høy andel tunge kjøretøy. I tillegg viser resultatene at tunneler med dype spor i gjennomsnitt har høyere friksjon. Den kombinerte effekten av økende spordybde og friksjon er at antall ulykker øker. Det betyr at virkningen av økende spordybden (økende antall ulykker hvis alt annet er lik) er større enn virkningen av økende friksjon (lavere antall ulykker hvis alt annet er lik).
Våt veg: På våt veg øker spor risikoen for vannplaning. Man kan derfor anta at økende spordybde medfører større ulykkesøkninger på våt veg enn på tørr veg (Chu & Fwa, 2016). Ingen av de empiriske studiene har imidlertid tallfestet effekten spesifikt for våt eller tørr veg.
Vinter: Det er vanskeligere å fjerne snø og is fra sporete veger. Dette kan gjøre kjøreforholdene vanskeligere om vinteren.
Andre mål på vegdekkets standard og ulykkesrisiko
De følgende studiene har undersøkt sammenhengen mellom andre mål for vegdekkets tilstand og antall ulykker:
Schandersson, 1981, 1989 (Sverige)
Anastasopoulos et al., 2008 (USA)
Cairney & Bennett, 2008 (Australia)
Chan et al., 2009 (USA)
Labi, 2011 (USA)
Buddhavarapu et al., 2013 (USA)
Li et al., 2013 (USA)
Lee et al., 2015 (USA)
Yokoo et al., 2016 (USA)
Wu et al., 2017 (Frankrike)
Xin et al., 2017 (USA)
Akbari et al., 2020 (Iran)
Himes & Donnell, 2020 (USA)
Cafiso et al., 2021 (Italia)
Siden alle studiene har benyttet ulike indikatorer for vegdekkets tilstand, er det ikke mulig å beregne gjennomsnittlige effekter. Vegdekkets tilstand er basert på ulike kombinasjoner av ujevnheter og skader (som f.eks. hull, sprekker og krakelering) og kan ha sammenheng med, men er ikke det samme som ujevnhet og spordybde. Det har heller ikke nødvendigvis sammenheng med vegdekkets friksjon.
Antall ulykker: De aller fleste resultatene viser at det er færre ulykker på veger med bedre dekker. En studie fant ingen sammenheng (Cafiso et al., 2021). En annen studie fant færre ulykker på noen typer veg («principal artierials») og ingen sammenheng på andre typer veg («major collector» og «minor arterial»).
Hull i vegen har i en studie vist seg å øke ulykkesrisikoen med 43% (95% konfidensintervall [+16; +77]; Khalili & Pakgohar, 2013).
Skadegrad: Li et al. (2013) viser at ulykker på gode vegdekker i gjennomsnitt er mer alvorlige enn ulykker på dårligere vegdekker.
Motorsykkelulykker: Én av studien har undersøkt sammenhengen mellom vegdekkets standard og antall motorsykkelulykker. Resultatene viser at det i gjennomsnitt er flere motorsykkelulykker på bedre vegdekker (Xin et al., 2017). Dette gjelder kurver på 2-feltsveger i spredtbygd strøk i Florida.
Virkninger på fremkommeligheten
Ujevnheter og skader i vegdekket fører til at kjørefarten settes ned (Anund, 1992; Bock et al., 2021; Karan, Haas & Kher, 1976; Hashim et al., 2018; Singh et al., 2011). Farten er også ofte høyere på helt nye vegdekker enn på eldre veger (Lyon, Persaud & Merritt, 2018).
Størrelsen på fartsendringen avhenger blant annet av trafikkmengden og hvor store ujevnhetene eller skadene i vegdekket er, men kan på mer enn 10 km/t (Hashim et al., 2018). King (2014) fant betydelig større overholdelse av fartsgrensen på veger med store ujevnheter (IRI over 4,6 mm per meter) og kun en svak eller ingen sammenheng mellom ujevnheter og fart på veger med mindre ujevnheter.
Veger med større ujevnheter og skader har også vist seg å ha større fartsvariasjon enn veger med god dekkestandard (Hashim et al., 2018).
Virkninger på miljøforhold
Det er ikke funnet undersøkelser som viser hvordan utbedring av ujevnheter i vegdekket påvirker miljøforhold. Ujevnheter i vegen kan føre til økt støy, for eksempel fra kjøretøy som kjører gjennom hull eller pga. oppbremsinger og akselerasjoner fra kjøretøy som prøver å unngå støt fra hull i vegen.
Kostnader
Kostnadene for bedring av vegdekkers ujevnhet og spor avhenger bl.a. av hvor store skader i vegdekket som skal repareres, hvor omfattende utbedringstiltak som blir gjort og av hvor store andeler av veglengden som utbedres.
Relevante kostnader som er knyttet til utbedringer av vegdekker, omfatter i hovedsak konstruksjons- og vedlikeholdskostnader, samt forsinkelser for trafikken i forbindelse med vegarbeider (Okte et al., 2019).
Nytte-kostnadsvurderinger
Det er ikke funnet noen nytte-kostnadsanalyser av utbedring av vegdekkers ujevnhet og spor. Vurderinger av nytte og kostnader ved generelle utbedringer av vegdekker som også vil medføre reduserte ujevnheter or spor, er beskrevet i kapittel 2.1.
Formelt ansvar og saksgang
Initiativ til tiltaket
Initiativ til utbedring av spor og ujevnhet tas som regel av vegmyndighetene på grunnlag av registreringer av vegdekkets tilstand som i tillegg til spor og ujevnhet også omfatter friksjon, sprekker, hull osv. Rapporter fra vegholder eller trafikanter om skader på vegdekket kan også utløse tiltak.
Formelle krav og saksgang
Statens vegvesens standard for drift og vedlikehold av riksveger fastsetter krav til vegdekker på riksveg (Statens vegvesen, håndbok R610, 2012). Disse kravene kan også gjøres gjeldende på fylkesveg, dersom fylkeskommunale myndigheter godtar dette. For kommunal veg kan kommunen utarbeide egen vedlikeholdsstandard for vegdekker.
R610 beskriver minstekravene som følgende:
- Spordybde: Spordybden skal være under 25 mm på veger med en trafikkmengde (ÅDT) under 5000 og under 20 mm på veger med ÅDT over 5000; dette gjelder 90-prosent-verdien av 20-meters-verdier for strekninger på 1 km lengde. Ingen slike verdier skal være over 40 mm.
- Ujevnheter: Maksimalverder for ujevnheter er definert for ulike trafikkmengder (fem grupper) og vegdekkeklasser (to klasser, en for riksveger og en for øvrige veger). Maksimalverdiene for riksveger ligger mellom 3,5 mm/meter i den høyeste trafikkmengdeklassen (ÅDT over 10.000) og 5,0 mm/meter i den laveste trafikkmengdeklassen (ÅDT under 300). Maksimalverdiene for andre veger ligger mellom 4,0 og 7,0 mm/meter. Maksimalverdiene gjelder 90-prosent-verdien av 20-meters-verdier for strekninger på 1 km lengde. Generelt skal ingen 20-meterverdier overskride kravet med mer enn 3 mm/meter.
I tillegg beskriver R610 maksimalverdier for friksjon (se kapittel 2.3), krakelering og sprekker.
Hvert år utarbeides en plan for hvilke veger som skal reasfalteres, og arbeidene legges ut på anbud. Planen er som regel basert på informasjon om dekketilstand, trafikkmengde og vegens viktighet (jf. kapittel 2.1).
Ansvar for gjennomføring av tiltaket
Vegholder er ansvarlig for gjennomføring av reasfaltering. Kostnadene dekkes av staten for riksveg, fylkeskommunen for fylkesveg og kommunen for kommunal veg.
Referanser
Abdelaziz, N., Abd El-Hakim, R. T., El-Badawy, S. M., & Afify, H. A. (2020). International Roughness Index prediction model for flexible pavements. International Journal of Pavement Engineering, 21(1), 88-99.
Akbari, M., Shafabakhsh, G., & Ahadi, M. R. (2020). Single-vehicle run-off-road crash prediction model associated with pavement characteristics. International journal of engineering, 33(7), 1375-1386.
Alacash, H. A. A., & Parry, T. (2019). Applying Random Parameters Model to Evaluate the Impact of Traffic, Geometric and Pavement Condition Characteristics on Accident Frequencies Occurred at A-Roads Networks in the UK. In Scientific And Technical Conference Transport Systems Theory And Practice (pp. 3-19). Springer, Cham.
Alhasan, A., Nlenanya, I., Smadi, O., & MacKenzie, C.A. (2018). Impact of pavement surface condition on roadway departure crash risk in Iowa. Infrastructures 3 (14).
Al-Masaeid, H.R. (1997). Impact of pavement condition on rural road accidents. Canadian Journal of Civil Engineering, 24, 523-531.
Al-Suleiman, T.I. & Shiyab, A.M. (2003). Prediction of pavement remaining service life using roughness data – Case Study in Dubai. International Journal of Pavement Engineering, 4 (2), 121–129.
Anastasopoulos, P. C., Mannering, F. L., Shankar, V. N., & Haddock, J. E. (2012). A study of factors affecting highway accident rates using the random-parameters tobit model. Accident Analysis & Prevention, 45, 628-633.
Anastasopoulos, P. C., Tarko, A. P., & Mannering, F. L. (2008). Tobit analysis of vehicle accident rates on interstate highways. Accident Analysis & Prevention, 40(2), 768-775.
Anastasopoulos, P.C., Mannering, F.L., Haddock,J. (2012). Random parameters seemingly unrelated equations approach to the post-rehabilitation performance of pavements. Journal of Infrastructure System 18(3), 176–182.
Anund, A. (1992). Vägytans inverkan på fordonshastigheter. VTI-meddelande 680. Väg- och TrafikInstitutet (VTI), Linköping.
Appiah, J., & Zhao, M. (2020). Examination of Features Correlated With Roadway Departure Crashes on Rural Roads (No. FHWA/VTRC 21-R2). Virginia. Dept. of Transportation.
Arhid et al., 2015;
Bock, M., Cardazzi, A., & Humphreys, B. R. (2021). Where the rubber meets the road: Pavement damage reduces traffic safety and speed (No. w29176). National Bureau of Economic Research.
Buddhavarapu, P., Banerjee, A., & Prozzi, J. A. (2013). Influence of pavement condition on horizontal curve safety. Accident Analysis & Prevention, 52, 9-18.
Cafiso, S., Montella, A., D’Agostino, C., Mauriello, F., & Galante, F. (2021). Crash modification functions for pavement surface condition and geometric design indicators. Accident Analysis & Prevention, 149, 105887.
Cairney, P. & Bennett, P. (2008). Relationship between Road Surface Characteristics and Crashes on Victorian Rural Roads. 23rd ARRB Conference, Adelaide, South Australia.
Cairney, P. & Styles, E. (2005). A pilot study of the relationship between macrotexture and crash occurence. Road Safety Research Report CR223. ARRB Transport Research Victoria, Australia.
Chan, C. Y., Huang, B., Yan, X., Richards, S. (2009). Relationship between highway pavement condition, crash frequency, and crash type. Journal of Transportation Safety and Security, 1, 268-281.
Chen, S., Saeed, T. U., Alqadhi, S. D., & Labi, S. (2019). Safety impacts of pavement surface roughness at two-lane and multi-lane highways: accounting for heterogeneity and seemingly unrelated correlation across crash severities. Transportmetrica A: transport science, 15(1), 18-33.
Christensen, P. & Ragnøy, A. (2006). Vegdekkets tilstand og trafikksikkerhet (The condition of the road surface and safety). TØI Report 840/2006. Oslo: Transportøkonomisk institutt.
Ding, Y., & Wang, H. (2018). Evaluation of hydroplaning risk on permeable friction course using tire–water–pavement interaction model. Transportation research record, 2672(40), 408-417.
Dong, C., Nambisan, S. S., Richards, S. H., & Ma, Z. (2015). Assessment of the effects of highway geometric design features on the frequency of truck involved crashes using bivariate regression. Transportation Research Part A: Policy and Practice, 75, 30-41.
Dysvik, E., Homleid, T., & Andreev, L. (2020). Kvaliteten på det norske veinettet – Status og utvikling for riks- og fylkesveier. Rapport 2020/38, Vista Analyse.
Elghriany, A., Yi, P., Liu, P., & Yu, Q. (2016). Investigation of the effect of pavement roughness on crash rates for rigid pavement. Journal of Transportation Safety & Security, 8(2), 164-176.
Ghanbari, A. (2017). Impact of pavement condition indicators on road safety in New Brunswick (Doctoral dissertation, University of New Brunswick.).
Hashim, I. H., Younes, M. A., & El-hamrawy, S. A. (2018). Impact of pavement condition on speed change for different vehicle classes. American Academic Scientific Research Journal for Engineering, Technology, and Sciences, 43(1), 271-290.
Hicks, R. G., Moulthrop, J. S., & Daleiden, J. (1999). Selecting a preventive maintenance treatment for flexible pavements. Transportation research record, 1680(1), 1-12.
Himes, S., & Donnell, E. (2020). Safety effects of horizontal curve reliability index. Transportation research record, 2674(9), 627-636.
Hou, Q., Tarko, A. P., & Meng, X. (2018A). Analyzing crash frequency in freeway tunnels: A correlated random parameters approach. Accident Analysis & Prevention, 111, 94-100.
Hou, Q., Tarko, A. P., & Meng, X. (2018B). Investigating factors of crash frequency with random effects and random parameters models: New insights from Chinese freeway study. Accident Analysis & Prevention, 120, 1-12.
Hussein, N., & Hassan, R. (2017). An assessment of safety at signalized intersections post resurfacing. International Journal of Transport Development and Integration, 1(2), 256-266.
Hussein, N., Hassan, R., & Fahey, M. T. (2021). Effect of pavement condition and geometrics at signalised intersections on casualty crashes. Journal of safety research, 76, 276-288.
Ihs, A., Gustafsson, M., Eriksson, O., Wiklund, M., & Sjögren, L. (2011). Road user effect models: the influence of rut depth on traffic safety. Statens väg-och transportforskningsinstitut. VTI rapport 731A.
Karan, M. A., R. Haas & R. Kher. (1976). Effects of Pavement Roughness on Vehicle Speeds. Transportation Research Record, 602, 122-127.
King, B.-A. (2015). The Effect of Road Roughness on Traffic Speed and Road Safety. Ph.D. dissertation, University of Southern Queensland, Australia, Nov. 2014
Kuleno, M. M., Kuma, D. K., & Reddy, R. R. (2019). Evaluating the Impacts of Pavement Surface Defects on Traffic Safety: A Case Study Between Arba Minch To Zeyise Wozeka Road, Ethiopia. IJRAR-International Journal of Research and Analytical Reviews (IJRAR), 6(1), 1256-1263.
Labi, S. (2011). Efficacies of roadway improvements across functional subclasses of rural two-lane highways. Journal of Safety Research, 42, 231-239.
Lee, J., Abdel-Aty, M., & Nyame-Baafi, E. (2020). Investigating the effects of pavement roughness on freeway safety using data from five states. Transportation research record, 2674(2), 127-134.
Lee, J., Nam, B., & Abdel-Aty, M. (2015). Effects of pavement surface conditions on traffic crash severity. Journal of Transportation Engineering, 141(10), 04015020.
Li, Y., Liu, C., & Ding, L. (2013). Impact of pavement conditions on crash severity. Accident Analysis & Prevention, 59, 399-406.
Lyon, C., Persaud, B. & Merritt, D. (2020). Developing crash modification factors and functions for high friction surface treatments on curves and ramps – an empirical Bayes before-after study. Transportation Research Record
Ma, X., Chen, F., & Chen, S. (2015). Modeling crash rates for a mountainous highway by using refined-scale panel data. Transportation research record, 2515(1), 10-16.
Ma, Z., Zhao, W., Chien, S.I.J., & Dong, C. (2015). Exploring factors contributing to crash injury severity on rural two-lane highways. Journal of safety research, 55, 171-176.
Mamlouk, M., Vinayakamurthy, M., Underwood, B. S., & Kaloush, K. E. (2018). Effects of the international roughness index and rut depth on crash rates. Transportation research record, 2672(40), 418-429.
Múčka, P. (2017). International Roughness Index specifications around the world. Road Materials and Pavement Design, 18(4), 929-965.
Nordahl, T. (2016). Kvaliteten på det norske veinettet, del 2 – status på riks- og fylkesveier. Oslo: Opplysningsrådet for veitrafikken.
Okte, E., Al-Qadi, I. L., & Ozer, H. (2019). Effects of pavement condition on LCCA user costs. Transportation Research Record, 2673(5), 339-350.
Piryonesi, S.M., & El-Diraby, T.E. (2021). Examining the relationship between two road performance indicators: Pavement condition index and international roughness index. Transportation Geotechnics, 26, 100441.
Popoola, M. O., Apampa, O. A., & Adekitan, O. (2020). Impact of Pavement Roughness on Traffic Safety under Heterogeneous Traffic Conditions. Nigerian Journal of Technological Development, 17(1), 13-19.
Pulugurtha, S. S., Ogunro, V., Pando, M. A., Patel, K. J., & Bonsu, A. (2013). Preliminary results towards developing thresholds for pavement condition maintenance: safety perspective. Procedia-Social and Behavioral Sciences, 104, 302-311.
Saeed, T. U., Hall, T., Baroud, H., & Volovski, M. J. (2019). Analyzing road crash frequencies with uncorrelated and correlated random-parameters count models: An empirical assessment of multilane highways. Analytic methods in accident research, 23, 100101.
Sarwar, M. T., & Anastasopoulos, P. C. (2017). The effect of long term non-invasive pavement deterioration on accident injury-severity rates: A seemingly unrelated and multivariate equations approach. Analytic methods in accident research, 13, 1-15.
Schandersson, R. (1981). Samband mellan vägbeläggningar och trafikolyckor 1977. VTI-meddelande 242. Linköping, Statens väg- och trafikinstitut (VTI).
Schandersson, R. (1989). Trafiksäkerhet och vägytans egenskaper (TOVE). En undersökning av belaga vägar med olika yttilstånd baserad på data från fyra nordiska länder 1982-1986. VTI-meddelande 594. Linköping, Statens väg- och trafikinstitut (VTI).
Semnarshad, M., Elyasi, M., Saffarzadeh, M., & Saffarzadeh, A. (2018). Identification and Prioritization of Accident-Prone Segments using International Roughness Index. International Journal of Transportation Engineering, 6(1), 35-48.
Singh, D., Zaman, M. M., & White, L. (2011). Modeling of 85th percentile speed for rural highways for enhanced traffic safety (No. FHWA-OK-11-07). Oklahoma. Dept of Transportation.
Start, M. R., J. Kim, & W. D. Berg. (1996). Development of safety-based guidelines for treatment of pavement rutting. In: Proceedings of the Conference Road Safety in Europe and Strategic Highway Research Program (SHRP), Prague, the Czech Republic, September 20-22, 1995, No 4A, Part 5, 79-98. Swedish National Road and Transport Research Institute, Linköping.
Statens vegvesen (2019). Vegdekker i region Øst 2019. Status for dekketilstand, kvalitet og kontrakter. SVV-Rapport Nr. 610.
Tegge et al., 2010
Tehrani, S. Sharif, and L Cowe Falls. (2012). A Comparison of IRI and Collision Rates in the Province of Alberta. Canadian Society for Civil Engineering. Canadian Society for Civil Engineering. 1024, 1.
Vinayakamurthy, M., Mamlouk, M., Underwood, S., & Kaloush, K. (2017). Effect of pavement condition on accident rate. Arizona State University.
Wu, D., Hours, M., & Martin, J. L. (2018). Risk factors for motorcycle loss-of-control crashes. Traffic injury prevention, 19(4), 433-439.
Xin, C., Wang, Z., Lin, P. S., Lee, C., & Guo, R. (2017). Safety effects of horizontal curve design on motorcycle crash frequency on rural, two-lane, undivided highways in Florida. Transportation research record, 2637(1), 1-8.
Yokoo, T., Levinson, D. M., & Marasteanu, M. (2016). Does poor road condition increase crashes? https://conservancy.umn.edu/bitstream/handle/11299/181548/Does%20poor%20road%20condition%20increase%20crashes.pdf?sequence=1&isAllowed=y

